Certifiably correct range-aided SLAM

Researchers in the Aerospace Controls Lab (ACL) introduce CORA, a novel algorithm for solving Range-Aided Simultaneous Localization and Mapping (RA-SLAM) problems in robotic navigation. The paper has been selected as the recipient of the 2024 IEEE Transactions on Robotics King-Sun Fu Memorial Best Paper Award.

Authors: Alan Papalia, Andrew Fishberg, Brendan W. O’Neill, Jonathan How, David M. Rosen, and John J. Leonard
Citation: IEEE Transactions on Robotics, Sept. 2024 (Volume: 40)

Abstract:
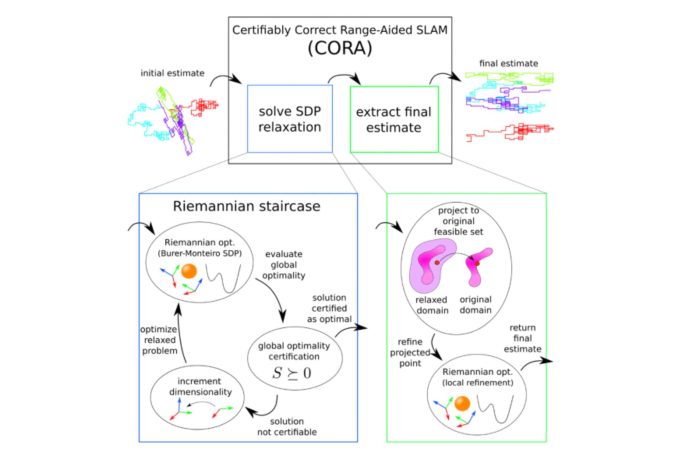
We present the first algorithm to efficiently compute certifiably optimal solutions to range-aided simultaneous localization and mapping (RA-SLAM) problems. Robotic navigation systems increasingly incorporate point-to-point ranging sensors, leading to state estimation problems in the form of RA-SLAM. However, the RA-SLAM problem is significantly more difficult to solve than traditional pose-graph SLAM: Ranging sensor models introduce nonconvexity and single range measurements do not uniquely determine the transform between the involved sensors. As a result, RA-SLAM inference is sensitive to initial estimates yet lacks reliable initialization techniques. Our approach, certifiably correct RA-SLAM (CORA), leverages a novel quadratically constrained quadratic programming formulation of RA-SLAM to relax the RA-SLAM problem to a semidefinite program (SDP). 

CORA solves the SDP efficiently using the Riemannian Staircase methodology; the SDP solution provides both: 1) a lower bound on the RA-SLAM problem’s optimal value and 2) an approximate solution of the RA-SLAM problem, which can be subsequently refined using local optimization. CORA applies to problems with arbitrary pose-pose, pose-landmark, and ranging measurements and, due to using convex relaxation, is insensitive to initialization. 

We evaluate CORA on several real-world problems. In contrast to state-of-the-art approaches, CORA is able to obtain high-quality solutions on all problems despite being initialized with random values. In addition, we study the tightness of the SDP relaxation with respect to important problem parameters: The number of: 1) robots; 2) landmarks; and 3) range measurements. These experiments demonstrate that the SDP relaxation is often tight and reveal relationships between graph connectivity and the tightness of the SDP relaxation.