Dimensionless learning based on information
Dimensional analysis helps scientists simplify complex systems by focusing on how quantities scale with one another, discovering common rules that apply to everything from a drop of water to a hurricane. Yuan Yuan (ACDL) and Professor Adrian Lozano-Duran use ideas from information theory—the science of how information is measured and transmitted—to improve dimensional analysis, discovering the most important dimensionless variables directly from data.
Authors: Yuan Yuan and Adrian Lozano-Duran
Citation: Nature Communications volume 16, Article number: 9171 (2025)
Abstract:
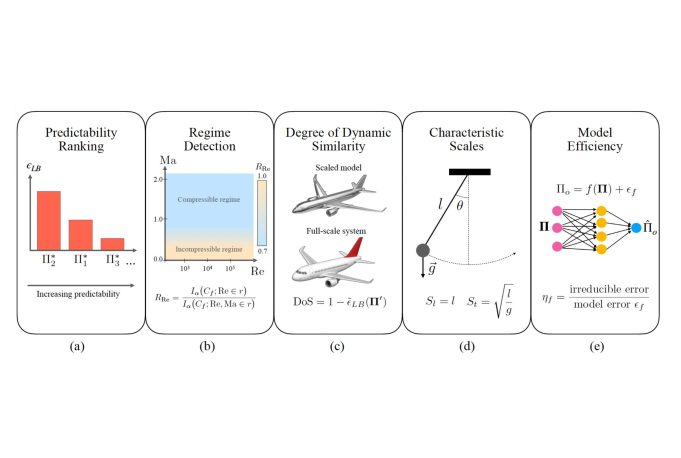
Dimensional analysis is one of the most fundamental tools for understanding physical systems. However, the construction of dimensionless variables, as guided by the Buckingham-π theorem, is not uniquely determined. Here, we introduce IT-π, a model-free method that combines dimensionless learning with the principles of information theory. Grounded in the irreducible error theorem, IT-π identifies dimensionless variables with the highest predictive power by measuring their shared information content.
The approach is able to rank variables by predictability, identify distinct physical regimes, uncover self-similar variables, determine the characteristic scales of the problem, and extract its dimensionless parameters. IT-π also provides a bound of the minimum predictive error achievable across all possible models, from simple linear regression to advanced deep learning techniques, naturally enabling a definition of model efficiency. We benchmark IT-π across different cases and demonstrate that it offers superior performance and capabilities compared to existing tools. The method is also applied to conduct dimensionless learning for supersonic turbulence, aerodynamic drag on both smooth and irregular surfaces, magnetohydrodynamic power generation, and laser-metal interaction.

