Uncertainty-aware Safe Exploratory Planning using Gaussian Process and Neural Control Contraction Metric
Abstract: Robots operating in unstructured, complex, and changing real-world environments should navigate and maintain safety while collecting data about its environment and updating its model dynamics. In this paper, we consider the problem of using a robot to explore an environment with an unknown, state-dependent disturbance to the dynamics and forbidden areas. The goal of the robot is to safely collect observations of the disturbance and construct an accurate estimate of the underlying function. We use Gaussian Process (GP) to get an estimate of the disturbance from data with a high-confidence bound on the regression error. Furthermore, we use neural Contraction Metrics to derive a tracking controller and the corresponding high-confidence uncertainty tube around the nominal trajectory planned for the robot, based on the estimate of the disturbance. From the robustness of the Contraction Metric, error bound can be pre-computed and used by the motion planner such that the actual trajectory is guaranteed to be safe. As the robot collects more and more observations along its trajectory, the estimate of the disturbance becomes more and more accurate, which in turn improves the performance of the tracking controller and enlarges the free space that the robot can safely explore. We evaluate the proposed method using a carefully designed environment with a ground vehicle. Results show that with the proposed method the robot needs a shorter time to thoroughly explore the environment and leads to fewer collisions.
Problem setup
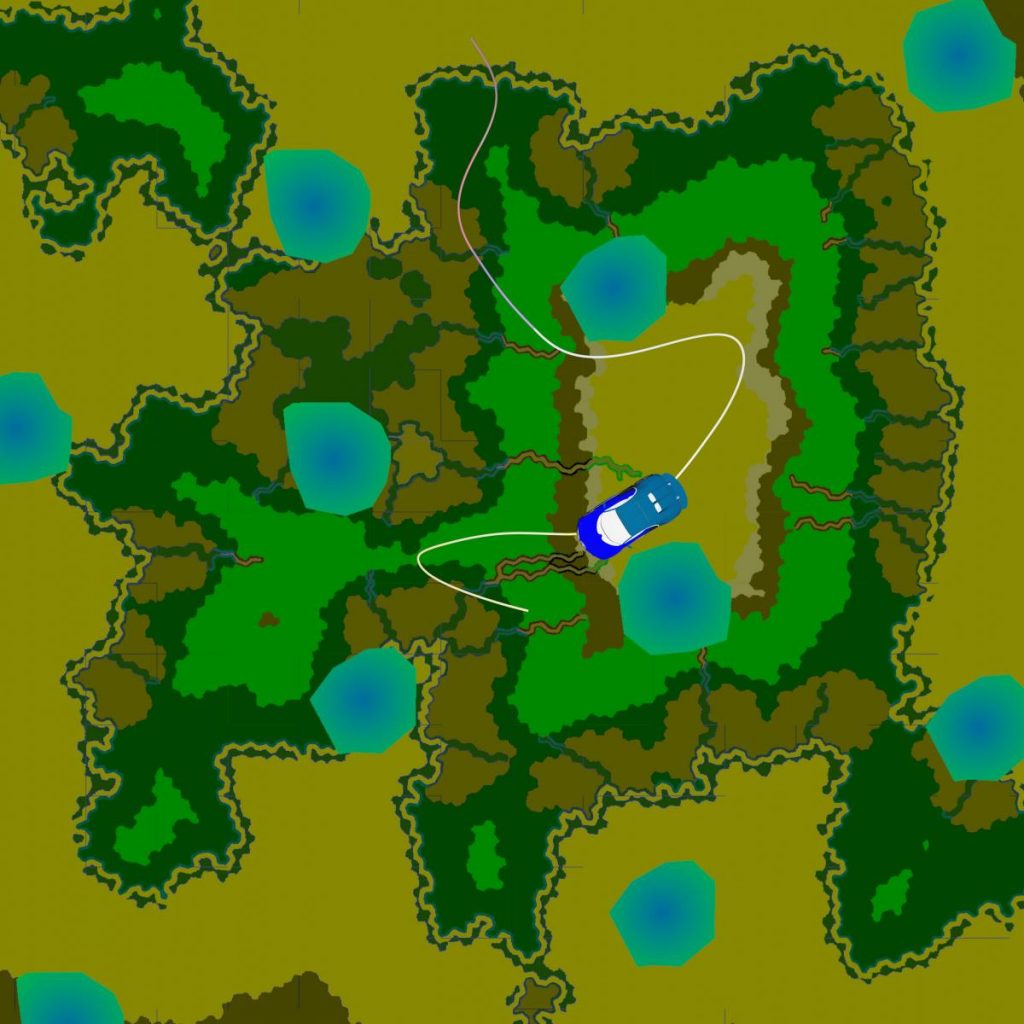
Motivating scenario: A ground vehicle needs to safely explore unseen environments to learn the effect of different terrains (in different colors) to its dynamics. The light blue regions are pools that the vehicle should avoid.
The vehicle has dynamics $\dot{x} = f(x) + B(x)u + d(x)$ where $d$ is the unknown model error. Before the exploration, we first learn a robust control law which consists of a controller and a contracting certificate. Together they can guarantee that the vehicle can track any desired path $x^*(t)$ while staying at most $\epsilon$ away from the desired path as long as uncertainty is bounded. Therefore, when planning for $x^*$, we just need to make sure that it is $\epsilon$ away from the forbidden area to guarantee safety. However, we do not have a sufficiently accurate prior knowledge of $d$. During exploration, $d$ will be learned using a GP model based on the samples along the traveled path of the vehicle. Initially, the vehicle is only aware of it surrounding environment. That is, it knows an upper-bound for the variance of $d$ in a ball with radius $\rho$ around itself. The vehicle will plan a path within the $\rho$-ball with the goal of obtaining more information about $d$. At each time step, the vehicle will collect samples along the traveled path to continue updating the GP model for $d$, which in turn improves the performance of the tracking controller. This process will terminate when the free space has been fully explored.
Safe exploration using GP and NCCM
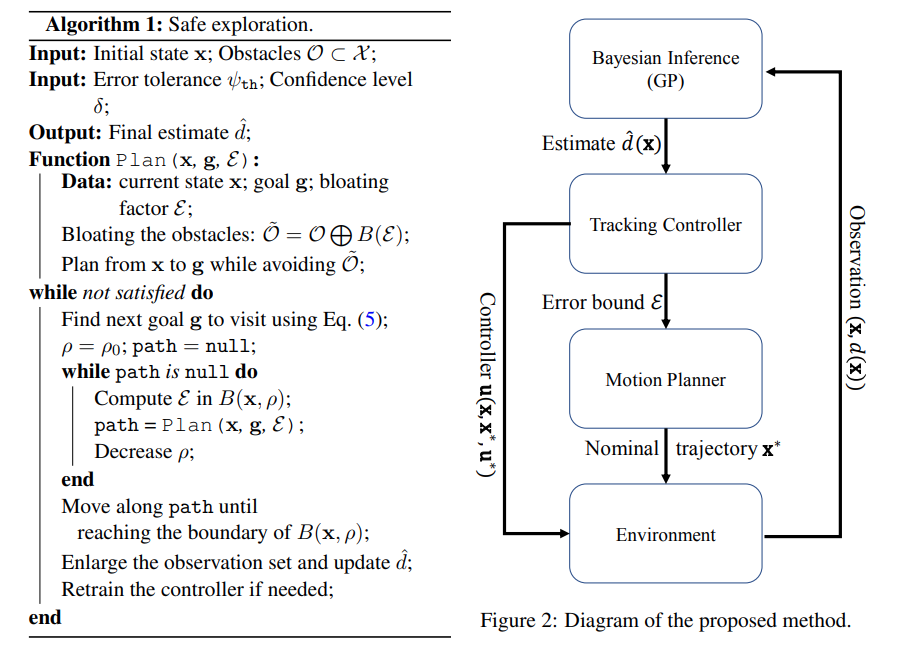
The proposed approach where GP is used to learn the unknown disturbance function from collected data and NCCM is used to plan safe path to the informative points.
