Scalable and Safe Multi-Agent Motion Planning with Disturbances

Abstract: We present a scalable and effective multi-agent safe motion planner that enables a group of agents to move to their desired locations while avoiding collisions with obstacles and other agents, with the presence of rich obstacles, high-dimensional, nonlinear, nonholonomic dynamics, actuation limits, and disturbances. We address this problem by finding a piecewise linear path for each agent such that the actual trajectories following these paths are guaranteed to satisfy the reach-and-avoid requirement. We show that the spatial tracking error of the actual trajectories of the controlled agents can be pre-computed for any qualified path that considers the minimum duration of each path segment due to actuation limits. Using these bounds, we find a collision-free path for each agent by solving Mixed Integer-Linear Programs and coordinate agents by using the priority-based search. We demonstrate our method by benchmarking in 2D and 3D scenarios with ground vehicles and quadrotors, respectively, and show improvements over the solving time and the solution quality compared to two state-of-the-art multi-agent motion planners.

2D Environment	3D Environment (Side)

Approach in a Nutshell

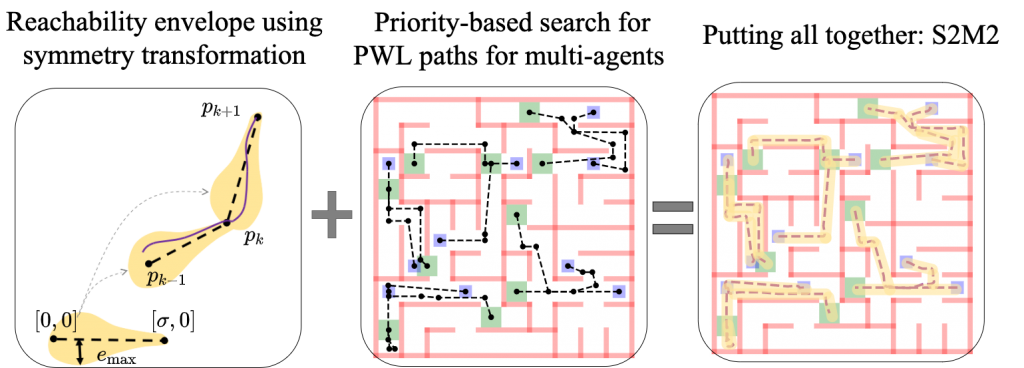
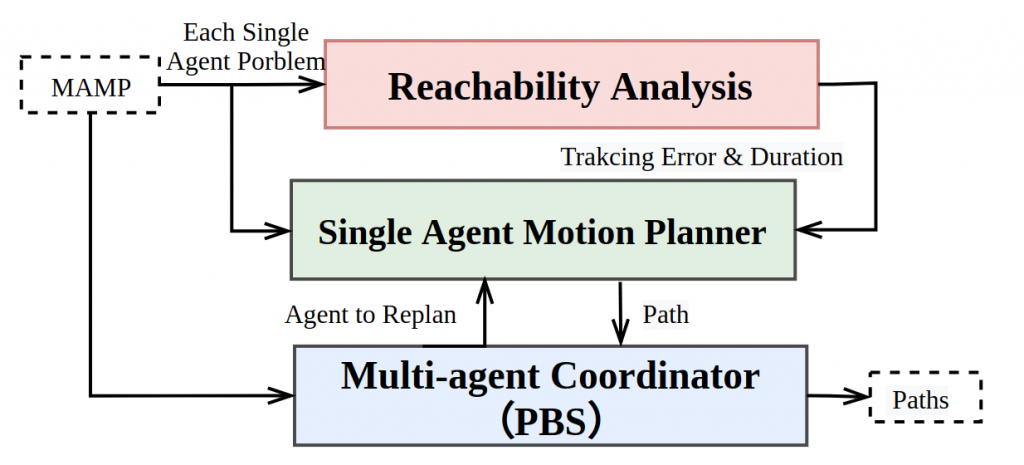
Our approach S2M2, consisting of three key modules: (a). Given a tracking controller for each agent, pre-compute reachability envelopes for any PWL path using symmetry transformations and cashed reachability envelopes, to get two key parameters: an upper bound of the spatial tracking error between the actual trajector and the minimum duration of each path segment such that the spatial tracking error bound is always valid. (b) Given two parameters from (a), the safe motion planning problem for each agent is reduced to finding a PWL path that is sufficiently far from the obstacles and other agents, which is further encoded as a MILP problem. (c) To coordinate multiple agents, employ priority-based search to avoid inter-robot collisions, in which some agents treat other agents as moving obstacles and replan their paths optimally.

Example

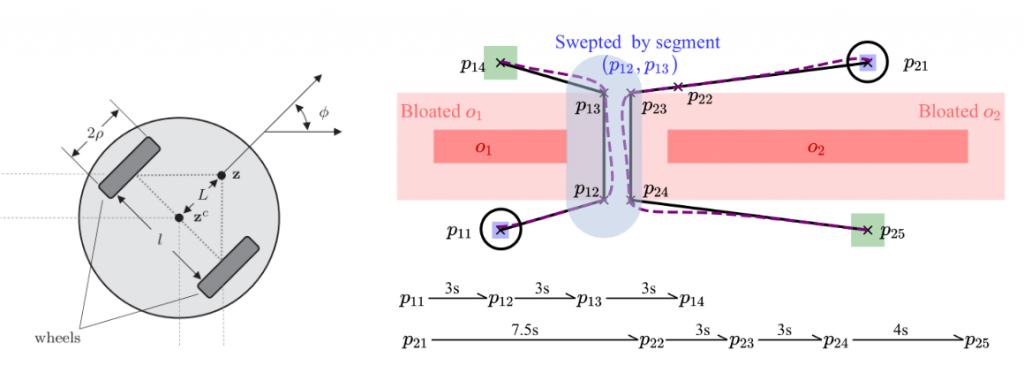
In our example, the agent model is a nonholonomic differential two-wheeled vehicle. Its state $\xi_i(t)$ consists of three components: $p(t) = [p_x(t), p_y(t)]^T$ is the Cartesian coordinate of the center of inertia, $\theta(t)$ is the angular orientation, and $v(t)$ is the linear velocity. We also consider the bounded disturbances $d_x$ on $p_x$, $d_y$ on $p_y$, and $d_\theta$ on $\theta$. The dynamic function $f_i$ is as follows is a nonlinear function. Consider an example of two disc-shaped vehicles making u-turns. Given the partially known initial locations and bounded disturbances, we first compute the spatial error bound of tracking a path segment, which is a line, and then consider this error together with the agent shape to obtain the possible swept area of the path segment. The swept area of agent $\mathcal{A}_1$ during its second segment $(p_{12}, p_{13})$ is shown in light blue. We also consider the minimum duration for each segment such that the agent has enough time to adjust its position after turning, which is $3$ seconds in our example. When our single-agent motion planner plans such paths for the agents, the obstacles are bloated with respect to the spatial tracking error and the agent shape, as shown in light red. The planner also constrains each segment to respect the minimum segment duration. As we can see, when passing the corridor, both agents slow down and use this $3$ seconds to adjust their trajectories. After passing the corridor, agent $\mathcal{A}_2$ uses its full speed to approach its goal location. When potential collisions are detected, some agents are assigned higher priorities and thus are treated as moving obstacles for others. In our example, agent $\mathcal{A}_1$ is assigned higher priority and thus passes the corridor before agent $\mathcal{A}_2$.

Experimental Results

We coimpare S2M2 against ECBS-CT and MAPF/C-Post on 2D and 3D scenarios, respectively. The results show S2M2 reduce the pre-computation time by up to three magnitudes, and it appears to be competitive in runtime and solution qualities.

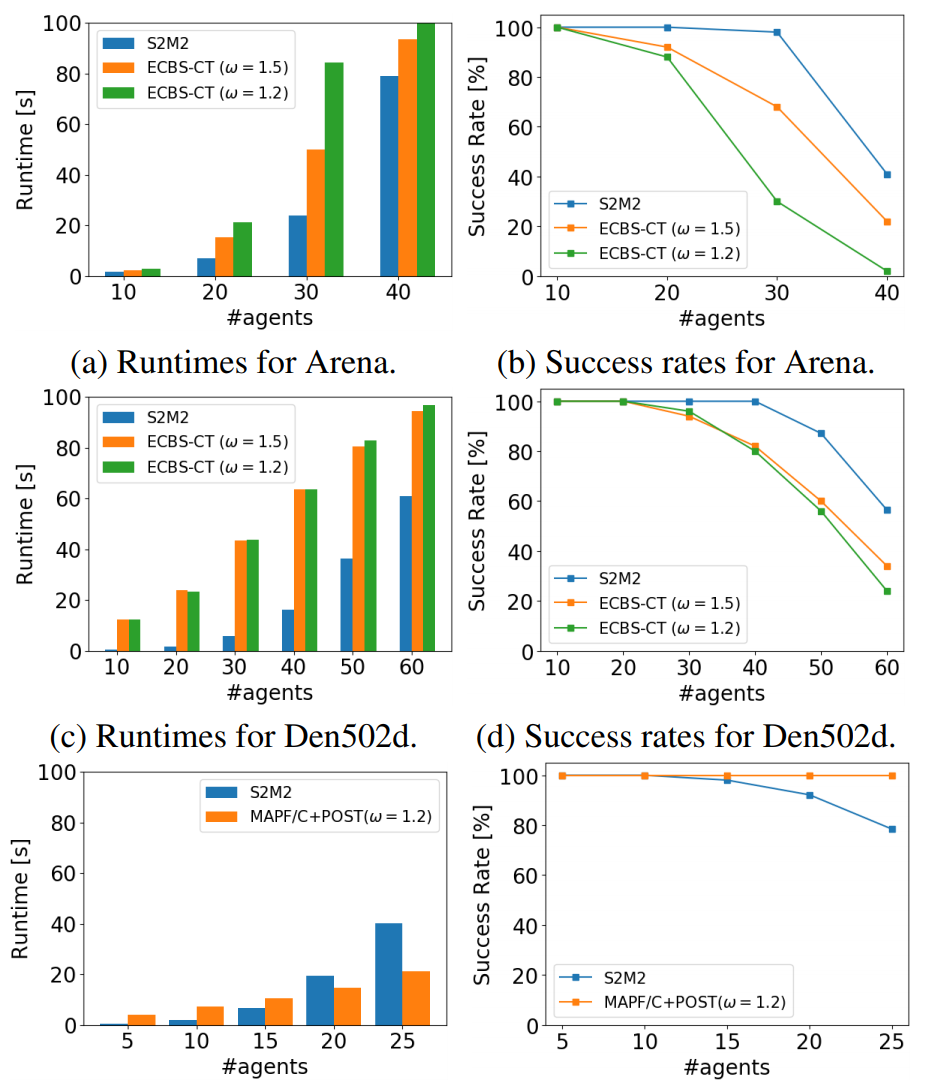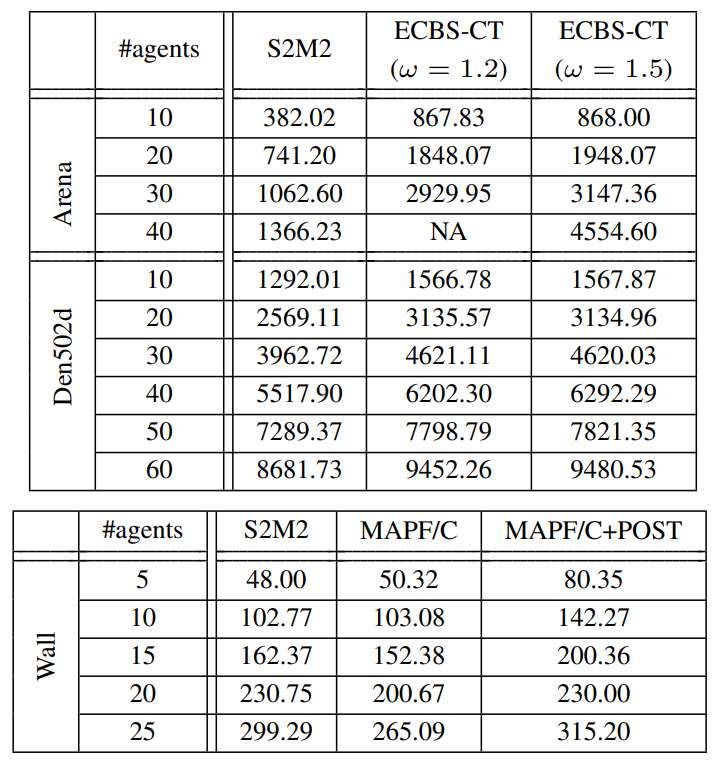Runtime and success rates.	Solution Qualities.