Density Constrained Reinforcement Learning
Abstract: We study constrained reinforcement learning (CRL) from a novel perspective by setting constraints directly on state density functions, rather than the value functions considered by previous works. State density has a clear physical and mathematical interpretation, and is able to express a wide variety of constraints such as resource limits and safety requirements. Density constraints can also avoid the time-consuming process of designing and tuning cost functions required by value function-based constraints to encode system specifications. We leverage the duality between density functions and Q functions to develop an effective algorithm to solve the density-constrained RL problem optimally and the constraints are guaranteed to be satisfied.
Introduction
Constrained reinforcement learning (CRL) aims to find the optimal policy that maximizes the cumulative reward signal while respecting certain constraints such as safety requirements and resource limits. Existing CRL approaches typically involve two crucial steps:
- Construct suitable cost functions and value functions to take into account the constraints.
- Choose appropriate parameters such as thresholds and weights for the cost and value functions to encode the constraints.
However, one significant gap between the use of such methods and solving CRL problems is the correct construction of the cost and value functions, which is typically not solved systematically but relies on engineering intuitions. Simple cost functions may not exhibit satisfactory performance, while sophisticated cost functions may not have clear physical meanings. When cost functions lack clear physical interpretations, it is difficult to formally guarantee the satisfaction of the performance specifications, even if the constraints on the cost functions are fulfilled. Moreover, different environments generally need different cost functions, which makes the tuning process time-consuming.
In this work, we study CRL from a novel perspective by imposing constraints on state density functions, which avoids the use of cost or value function-based constraints in previous CRL literature. Density is a measurement of state concentration in the state space, and is directly related to the state distribution. A variety of real-world constraints are naturally expressed as density constraints in the state space. For example, safety constraints is a special case of density constraints where we require the entire density distribution of states being contained in safe regions. Resource limits can also be encoded by imposing maximum allowed density on certain states.
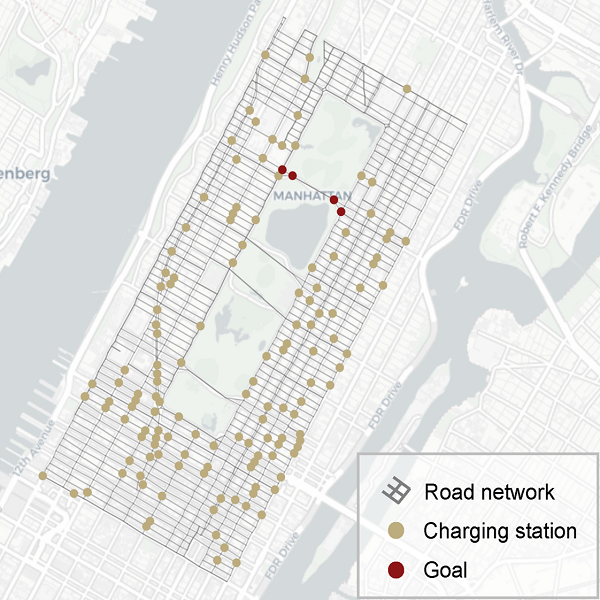
As an illustration of the density constraint, we consider the electrical vehicle (EV) routing task in the city of Manhattan shown in the figure above. The road network is marked as grey grids. Hundreds of EVs are controlled to transport passengers from random locations to the goals. To prevent running out of power, the EVs can be charged at charging stations denoted by brown dots. There are two constraints in this scenario:
First, the EVs do not run out of power. They need to be charged at charging stations when necessary. Second, the vehicle density at any charging station should not exceed the maximum allowed density. The resource is limited. The EVs should also optimize the total time of traveling from the starting locations to the goals. Both constraints can be expressed as density constraints. The first constraint can be realized by restricting the density of low-power states to 0. The second constraint can be realized by restricting the vehicle density at each charging stations to be below the threshold.
There are two advantages of density constraint over the existing value function-based constraints:
- Density has a clear physical and mathematical interpretation as a measurement of state concentration in the state space. A wide range of real-world constraints can be conveniently expressed as density constraints (e.g., the vehicle density in certain areas, and the frequency of agents entering undesirable states). The user-specified requirements can be conveniently converted into density constraints.
- Existing value function constraint requires the time-consuming process of designing and tuning cost functions, which are completely avoided by the density constraint since no cost function tuning is needed.
We also show in Section 4 of our paper that existing value function-based constraint is indeed a special case of density constraint. Density constraint is much more expressive.
Formulation of Density Constraint Reinforcement Learning
State density functions measure the state concentration in the state space. For infinite horizon MDPs, given a policy π and an initial state distribution ϕ the stationary density of state s is expressed as:State density functions measure the state concentration in the state space. For infinite horizon MDPs, given a policy π and an initial state distribution ϕ the stationary density of state s is expressed as:
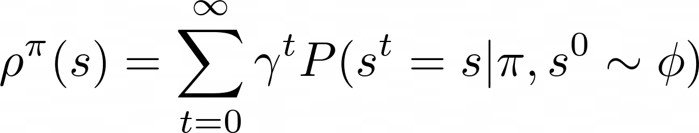
which is the discounted sum of the probability of visiting s. Given the initial state distribution ϕ and the state-wise density constraint ρ_min and ρ_max, the Density Constraint Reinforcement Learning problem finds the optimal solution to:
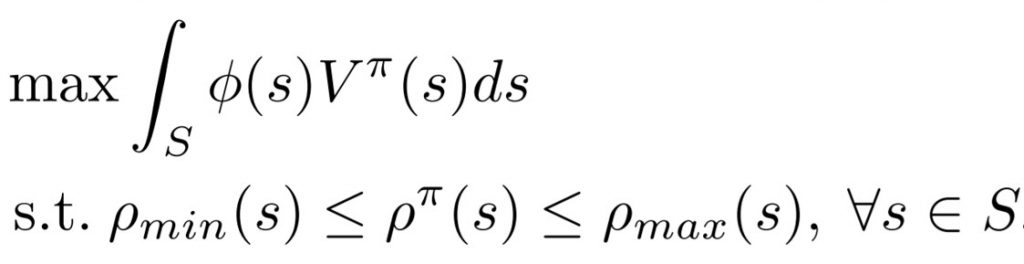
which maximizes the expected cumulative reward subject to the per-state constraint on state density.
Algorithm for DCRL
To solve the DCRL problem, we cannot directly apply existing RL algorithms, which are designed to optimize the expected cumulative reward or cost, but not the state density function. However, we show that density functions are dual to Q functions, and the density constraints can be realized by modifying the formulation of Q functions. Then the off-the-shelf RL algorithms can be used to optimize the modified Q functions to enforce the density constraints.
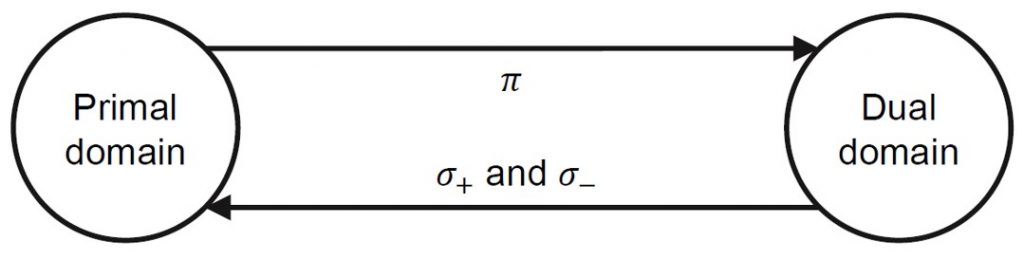
By utilizing the duality between density function and Q function, in the density constrained optimization, the DCRL problem can be solved by alternating between the primal problem and dual problem. We will not dive into details of the algorithm in this blog. Please refer to Section 4 of our paper for the proposed DCRL algorithm.
Experiments
We consider a wide variety of CRL benchmarks and demonstrate how they can be effectively solve by the proposed DCRL approach. The density constrained benchmarks include autonomous electrical vehicle routing, safe motor control, and agricultural drone control. The standard CRL benchmarks are from MuJoCo and Safety-Gym.
Three state-of-the-art CRL methods are compared. PCPO first performs an unconstrained policy update then project the action to the constrained set. CPO maximizes the reward in a small neighbourhood that enforces the constraints. RCPO incorporates the cost terms and Lagrange multipliers with the reward function to encourage the satisfaction of the constraints.
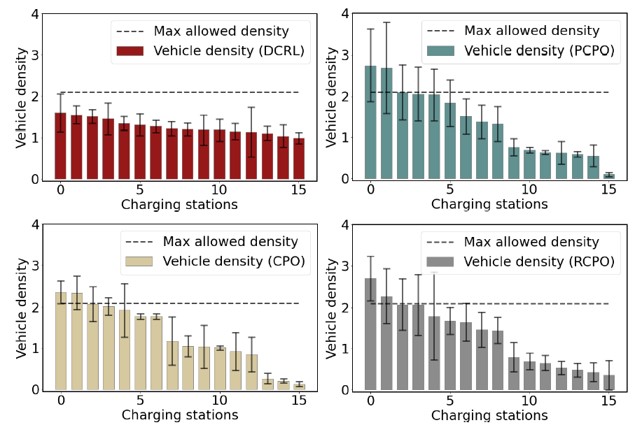
Electrical vehicle routing in Manhattan. While EVs drive to their destinations, they can avoid running out of power by recharging at the fast charging stations along the roads. At the same time, the vehicles should not stay at the charging stations for too long in order to save resources and avoid congestion. An road intersection is called a node. In each episode, an autonomous EV starts from a random node and drives to the goals. At each node, the EV chooses a direction and reaches the next node along that direction at the next step. The consumed electric energy is assumed to be proportional to traveling distance. Two types of constraints are considered: (1) the minimum remaining energy should keep close to a required threshold and (2) the vehicle density at charging stations should be less than a given threshold. The demonstrates that our DCRL can avoid the vehicle densities from exceeding the thresholds, while the baseline methods suffer from constraint violation. This is because DCRL allows us to explicitly set state density thresholds.
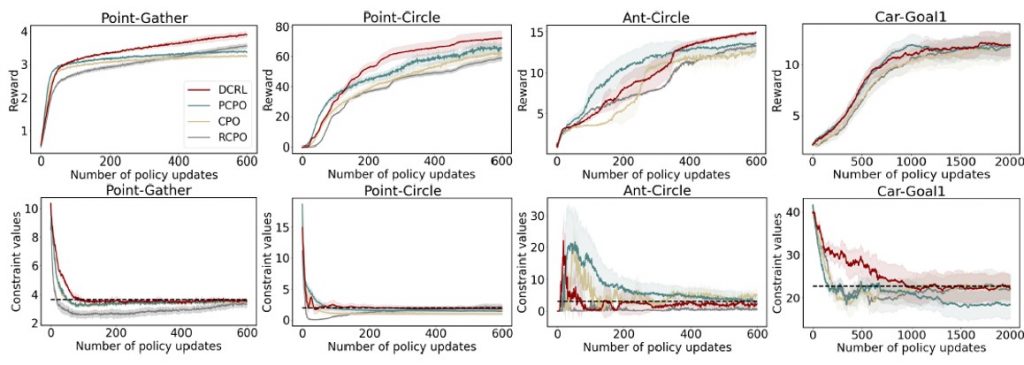
MuJoCo and Safety-Gym. Experiments are conducted on three tasks adopted from CPO and two tasks from the Safety-Gym, built on top of the MuJoCo simulator. The tasks include Point-Gather, Point-Circle, Ant-Circle, Car-Goal and Car-Button. The above figure demonstrates the performance of the four methods. In general, DCRL is able to achieve higher reward than other methods while satisfying the constraint thresholds. In the Point-Gather and Point-Circle environments, all the four approaches exhibit stable performance with relatively small variances. In the Ant-Circle environment, the variances of reward and constraint values are significantly greater than that in Point environments, which is mainly due to the complexity of ant dynamics. In Ant-Circle, after 600 iterations of policy updates, the constraint values of the four approaches converge to the neighbourhood of the threshold. The reward of DCRL falls behind PCPO in the first 400 iterations of updates but outperforms PCPO thereafter.
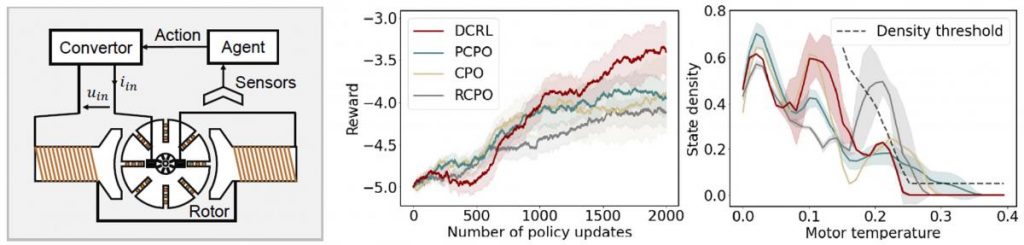
Safe Motor Control. The objective is to control the direct current series motor and ensure its angular velocity follows a random reference trajectory and prevent the motor from overheating. The agent outputs a duty cycle at each time step to drive the angular velocity close to the reference. When the reference angular velocity increases, the required duty cycle will need to increase. We consider the state density w.r.t. the motor temperature as constraint. High-temperature states should have a low density to protect the motor. We find that DCRL is successful at reaching the highest reward among the compared methods while respecting the state density constraints. More experiments under different settings can be found in the supplementary material.
